Estudio de correlaciones cuánticas
Steering.
Dos sistemas físicos separados (sin interacción entre ellos) pueden no obstante presentar correlaciones que van mas allá de las permitidas por la física clásica. Estas correlaciones Cuánticas son consecuencia del entrelazamiento, esto es el hecho de que en Mecánica Cuán-tica el estado de un sistema de dos partes no es necesariamente el producto de los estados de cada parte [Fel17][You20].
Una forma de generar dos haces de luz entrelazados es enviar un haz de luz no-clásico (luz comprimida) a un divisor de haz en inglés «beamsplitter» (BS). A la salida del BS los haces de luz están (generalmente) entrelazados. Considerando este sistema, estudiamos experi-mentalmente y teóricamente las correlaciones cuánticas producidas determinando el valor de diferentes cuantificadores de estas correlaciones [Val14].
Un tipo muy particular de correlaciones cuánticas lo constituye el fenómeno de «steering», esto es la posibilidad de que las medidas efectuadas en un sistema afecten el estado del otro. Contrariamente a las demás correlaciones, este efecto puede ser unidireccional. Para ciertos estados del conjunto, una parte puede afectar (pilotear) la otra sin que la recíproca sea cierta. Motivados por el estudio experimental, analizamos teóricamente en detalle la posibilidad de steering entre estados Gaussianos para estados simétricos (obtenibles con un BS de 50% de transmisión/reflexión). Identificamos el conjunto de todos los estados simétri-cos para los que el steering es posible mediante la utilización de observables Gaussianos y mostramos que en ciertos casos otros observables (no-Gaussianos) pueden ser más eficientes que los Gaussianos [Ben22].
No-localidad.
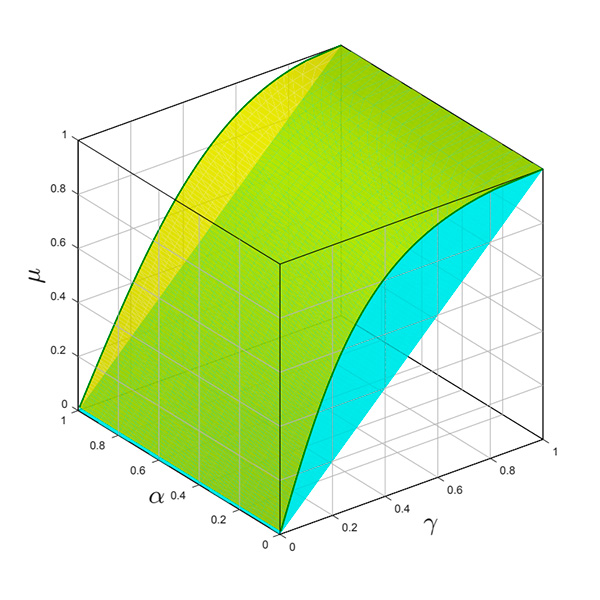
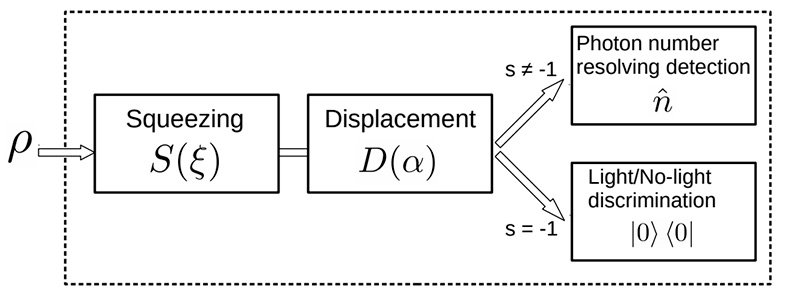
Una particularidad de los estados Gaussianos es que presentan distribuciones de quasi-probabilidad con caracterísiticas clásicas. Durante un tiempo se pensó que esto tornaría imposible la violación de las desigualdades de Bell que deben ser verificarse en los resultados de medidas realizadas sobre un sistema con dos partes cuando estos están determinados por condicionantes locales. Sin embargo la violación de la desigualdades de Bell y por consiguiente la demostración de no-localidad puede efectuarse mediante la utilización de medidas (observables) particulares. Nuestro aporte ha consistido en introducir una nueva familia de observables que permiten la observación de no-localidad. Estos observables se basan en la compresión (squeezing) de los estados recibidos por ambas partes. Como caso particular, estos observables permiten una im-plementación sencilla consistente en la compresión seguida de la detección de luz u oscuridad. [Lez23].
[Fel17] «Direct-dynamical Entanglement–Discord relations«, V. Feldman, J. Meziero, A. Auyuanet. Quantum Inf Process 16:128 (2017).
[You20] “Entanglement–Coherence and Discord–Coherence analytical relations for X states«. J. D Young and A. Auyuanet, Quantum Information Processing 19, 398 (2020).
[Val14] “Experimental characterization of the Gaussian state of squeezed light obtained via single-passage through an atomic vapor«, P. Valente, A. Auyuanet, Barreiro, H. Failache, A. Lezama. Phys. Rev. A, 91, 053848 (2015).
[Ben22] «Einstein-Podolsky-Rosen steering in symmetrical Gaussian states«. E. Benech, A. Auyuanet, and A. Lezama. Phys. Rev. A 106, 042201 (2022).
[Lez23] “Bell non-locality in two-mode Gaussian states revealed via local squeezing”. A. Lezama and A. Auyuanet, Physical Review A, 108, 052219 (2023).